Tower Of Hanoi

Today I will try to explain the Tower Of Hanoi Algorithm in Full detail. I don’t want you to just mug up the 3 lines of code and pass an exam . I want you to learn How we reach to the solution. How we decompose the problem and recompose it again to get the solution which is very important to solve a problem like this. You will also learn how to apply the recursion to get the desired solution.

Tower Of Hanoi:- The problem description is as follows:

We have Three pillars/pegs and N discs of different size on One pillar/peg such that They are in Incresing order of size from top to bottom.

What we have to do?

We have to move the Discs from  Source Peg to  Destination Peg  keeping the following constraints in Mind.

Constraints:

1.)We can take one peg out at a time.

2.)We can’t place small disc below the larger one during the task.

3.)We can only use one more pillar for help to complete the solution.

Problem:

Solution:

We have described the problem the solution above. Now we have to think how to solve the same.

Let Us decompose the problem and try to solve it 

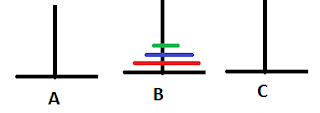
Let us Assume that we have only one Disc On peg A and We have to move the same to the Peg B.The solution is obvious , We will just pick the disc and put it on B and the problem is solved , let us see the same in Picture.

Solution of 1 disc Problem

(1,A,B,C) denotes that we have moved 1 disc from A to B using C.

SO, (1,A,B,C) solves the One Disc Problem.

Now , Let Us Assume that We have Two Disc and We have to move both disc from A to B. Let us see the solution of Two Disc Problem in Picture.

Solution Of 2 Discs problem

So, To solve 2 Disc problem we have followed the following 3 steps:

1.) (1,A,C,B)

2.) (1,A,B,C)

3.) (1,C,B,A)

Now Let us Take the 3 Disc Problem, Now we have to move the 3 discs from A to B.

Solution of 3 Disc Problem:

Now if We see The solution of 2 Disc Problem(2,A,B,C) is :

1) (1,A,C,B)  

2.) (1,A,B,C)

3.) 1(C,B,A)

So,The First 3 steps:

1.) (1,A,B,C)

2.) (1,A,C,B)

3.) (1,B,C,A)

 of the 3 disc problem is the solution of Problem (2,A,C,B)

And,The 4th Step:

4.) (1,A,B,C)

is the solution of Problem(1,A,B,C)

And the last 3 steps:

5.) (1,C,A,B)

6.) (1,C,B,A)

7.) (1,A,B,C)

is the solution of Problem(2,C,B,A)

So the solution of 3 disc problem(3,A,B,C) can be written as:

1.) (2,A,C,B)

2.) (1,A,B,C)

3.) (2,C,B,A).

and Similarly the solution of N disc problem(n,A,B,C) can be written as:

1.) (n-1,A,C,B)

2.) (1,A,B,C)

3.) (n-1,C,B,A).

So, In this way we have decomposed the problem into three parts to solve it.

Now let us say 

A-->From

B-->To

C-->Via

So the Tower of hanoid problem is (N,From,To,Via) which can be solved in three steps:

1.) (n-1,From,Via,To) -- first solve the problem of moving n-1 discs From to Via .

2.) (1,From,To,Via) -- Then solve the problem of moving 1 disc From to To.

3.) (n-1,Via,To,From) -- Then Solve the problem of moving n-1 disc from Via to To back.

We can also draw the Recursion Tree of the problem Here.